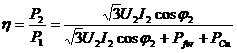Electronique, Electrotechnique et Machines Electriques

 

 

 

Les avantages de distribution d’énergie électrique en courant alternatif sont multiples :

-          La transformation de la tension et de l’intensité du courant est facile ;

-          Les générateurs de courant alternatif sont plus simples et ont un meilleur rendement que les générateurs de courant continu ;

-          Les à courant alternatif sont plus économiques et de construction moins compliquée que les moteurs à courant continu ;

-          La coupure d’un arc de courant alternatif se fait plus facilement que celle d’un arc de courant continu ;

-          Le courant alternatif peut être aisément transformé en courant continu par des redresseurs.

 

I-     Propriétés du courant alternatif

 

1.      Définitions :

·               On appelle courant alternatif un courant qui change périodiquement d’intensité et de sens. La polarité s’inverse donc constamment.

Dans le cas d’un régime sinusoïdal, la tension et l’intensité du courant varient en fonction du temps selon une loi sinusoïdale.

 

 

 

 

·               La vitesse angulaire w, ou pulsation, est l’angle (en radians) parcouru par seconde :

 

(w en radians par seconde, rd/s ou rad/s).

 

·                          La valeur instantanée u ou i est la valeur de la tension ou du courant à un instant donné ;

 

q_u et q_i sont respectivement les déphasages à l’origine de la tension u et du courant i.

 

·                    La valeur de crête ou amplitude Û ou Î est la valeur maximale de la tension ou du courant atteinte au cours d’une période ;

·                    La valeur moyenne U_moy ou I_moy est la moyenne arithmétique des valeurs instantanées de la tension ou du courant pendant une période

 

 

Pour un courant sinusoïdal, la valeur moyenne est nulle.

 

-              La courbe pendant laquelle les valeurs instantanées du courant sont positives est dite alternance positive ;

-              La courbe pendant laquelle les valeurs instantanées du courant sont négatives est dite alternance négative ;

-              La période T est le temps nécessaire pour obtenir deux alternances complètes, l’une positive, l’autre négative. La période T s’exprime en seconds (s).

-              La fréquence f est le nombre de périodes par seconde

T en secondes (s)

 

Quelques exemples de fréquences utilisées selon le domaine d’application du courant alternatif :

- Distribution d’énergie 50 Hz

- Moteurs à grande vitesse 100 Hz …. 400 Hz

- Electro-acoustique 16 Hz…….16 KHz

- Ultra –son 20 KHz……100 KHz

- Radiotélévision 100 KHz…..1GHz

- Faisceau 1 GHz et plus

- La valeur efficace I d’un courant alternatif est égale à l’intensité du courant continu qui produirait la même quantité de chaleur dans la même résistance pendant le même temps.

On démontre que dans le cas d’un courant sinusoïdal :

 

, soit

, soit

 

2.      Représentation graphique d’un signal sinusoïdal :

 

On considère le cercle trigonométrique de rayon qui évolue à une vitesse angulaire W, dans le sens inverse des aiguilles d’une montre. La translation de la rotation du rayon reproduit une courbe sinusoïdale en fonction de l’angle.

 

 

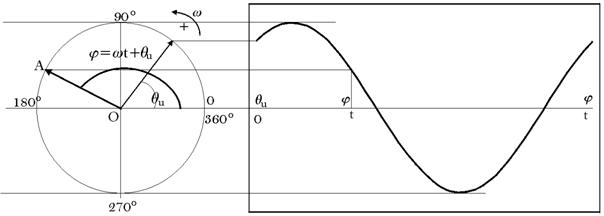
Le rayon OA est le vecteur qui représente la grandeur sinusoïdale.

Un vecteur est caractérisé par :

- Son point d’application ;

- Sa longueur ;

- Sa direction ;

- Son sens d’orientation.

 

3.      Grandeurs sinusoïdales de même fréquence :

a.                                    Deux tensions alternatives sinusoïdales sont en phase lorsqu’elles atteignent simultanément leurs valeurs de crête positives et négatives, dans ce cas, leurs vecteurs ont le même point de rotation, une longueur proportionnelle à la valeur de la tension et tournent à la même vitesse et dans le même sens.

 

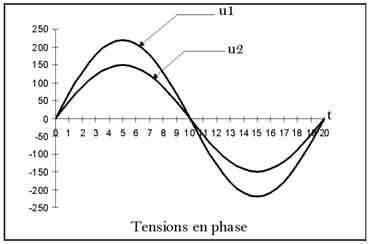
b.                                    Deux tensions alternatives sinusoïdales u₁ et u₂ sont déphasées lorsqu’elles n’atteignent pas simultanément leurs valeurs de crêtes positives et négatives. Les vecteurs tournent avec un retard de l’un par rapport à l’autre.

 

 

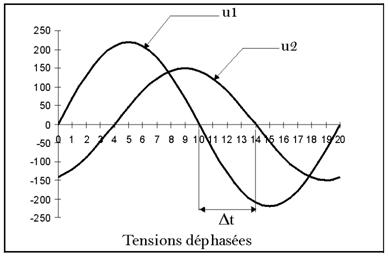
La tension u₂ atteint sa valeur de crête positive après un temps Dt par rapport à u₁, on dit que u₂ est déphasée en arrière par rapport à u₁. Le déphasage j est mesuré en degrés.

Dt est le décalage horaire entre les deux tensions.

La relation entre le déphasage j et le décalage horaire Dt est donnée par :

 

c.      Cas particuliers :

·           : les grandeurs sont en phase ;

·          : Les grandeurs sont en quadrature de phase ;

·           : Les grandeurs sont en opposition de phase.

 

4.      Représentation de Fresnel :

 

La représentation de Fresnel est une représentation vectorielle des grandeurs sinusoïdales.

La représentation d’un vecteur peut se faire :

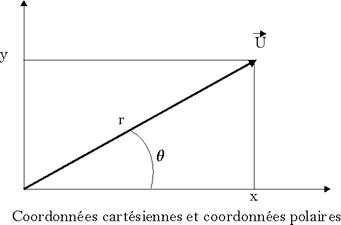
·         En coordonnées cartésiennes, on doit connaître la position (x, y) de l’extrémité du vecteur par rapport à son origine.

·         En coordonnées polaires, on doit connaître sa longueur et l’angle qu’il fait avec un axe d’origine.

 

 

II- Circuits linéaires en régime sinusoïdal

 

1.      Circuit résistif

 

Dans un circuit purement résistif, les valeurs instantanées du courant et de la tension sont proportionnelles et en phase. La loi d’Ohm s’écrit donc :

 

u(t) = Ri(t)

 

 

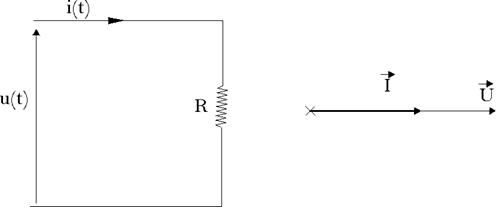
Dans ce cas, on peut utiliser les valeurs efficaces ou celles de crête :

 

U = RI ou Û = RÎ

 

2.      Circuit inductif (cas d’une bobine idéale R = 0)

 

On considère que l’inductance L est parcourue par un courant i de la forme : et on admet que la tension aux bornes de la bobine s’écrit :

 

 

Ce qui donne :

 

De cette relation on peut tirer deux enseignements :

-          u(t) et i(t) sont en quadrature de phase, u est en avance de sur i ;

-          , où est la réactance d’induction, elle s’exprime en ohms (W).

 

 

 

 

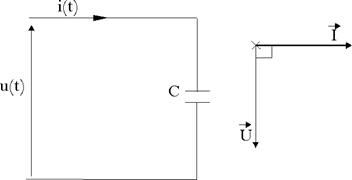
3.      Circuit capacitif

 

On considère que u est de la forme : u(t) = Ûsin(wt), et on admet que : .

Ce qui donne :

 

 

Le courant est donc en quadrature de phase avance par rapport à la tension, autrement dit, la tension est en quadrature de phase retard par rapport à i.

D’une part, , ou encore , et d’autre part

soit

 

L’expression représente la réactance de capacité notée, et exprimée en ohms (W).

La réactance de capacité est égale à l’impédance du condensateur.

 

Remarque :

Si l’on prend l’intensité du courant i(t) comme référence de phase, on aura :

, et

 

 

 

4.      Cas d’une bobine réelle () :

 

 

On prend

 

D’après la loi de Kirchoff des tensions, on a :

 

Avec et

 

 

D’après cette représentation, on peut écrire :

ou encore

Et

 

Le terme est une combinaison de la résistance propre de la bobine et de sa réactance, on l’appelle impédance et on la note Z.

 

 

Le déphasage de la tension par rapport à l’intensité du courant, introduit par l’impédance Z, est :

 

 

Exemple :

Une bobine d’une résistance de 1W a une inductance de 0,07H pour un courant de 1A.

Calculer son impédance et sa réactance d’induction pour une fréquence de 50 Hz, ainsi que le déphasage j.

 

Réponse :

 

 

 

 

 

I-     Puissance instantanée et puissance moyenne

 

On considère un circuit électrique dont la tension à ses bornes soit et le courant qui le traverse soit.

Entre les instants t et t+dt l’énergie consommée par ledit circuit est :

 

La puissance P est donnée par :

C’est une fonction sinusoïdale qui varie autour de la valeur constante avec la pulsation.

 

La valeur est la valeur moyenne de la puissance instantanée :

La valeur UI est appelée puissance apparente, on la note S et on l’exprime en VA (voltampères).

On a donc : , et

-          si, P=S ;

-          si, P=0 ;

Remarque :

On peut avoir un circuit parcouru par un courant, sans pour autant qu’il consomme de l’énergie.

 

II-  Etude de la puissance moyenne dans différents cas :

 

1.      Générateur (alternateur)

Soit et la tension et le courant qu’il délivre, la puissance moyenne fournie par le générateur est :

Elle est égale, aux pertes d’énergie mécanique près, à la puissance mécanique qu’il faut fournir pour le faire fonctionner.

 

 

 

1.      Moteur

2.      Résistance non inductive

, et

 

 

3.      Inductance pure

, et.

 

4.      Bobine réelle

 

La puissance consommée résulte uniquement de l’effet Joule dans la résistance.

 

5.      Condensateur

, et.

6.      Circuit R-L-C série

 

La puissance consommée résulte uniquement de l’effet Joule dans la résistance.

 

 

III- Puissance active et puissance réactive

 

La puissance consommée dans un circuit est appelée puissance active (on dit aussi puissance réelle).

Pour la commodité de certains calculs, on fait intervenir une puissance fictive, qu’on appelle puissance réactive.

On a donc :

On considère un circuit électrique traversé par le courant et soumis à la tension.

Ce courant peut s’écrire :

Avec :

, en phase avec la tension appelé aussi courant watté ;

, en quadrature de phase sur la tension, appelé aussi courant déwatté ;

-          La puissance moyenne du courant watté est la puissance active P ;

-          La puissance moyenne du courant déwatté est nulle ;

-          La puissance réactive est la puissance apparente du courant déwatté ;

-          Dans une inductance pure, le courant est entièrement déwatté et l’on écrit :

,  ;

-          Dans un condensateur, on :

,  ;

La puissance réactive est négative, on dit que le condensateur fournit de l’énergie réactive au reste du circuit.

Dans le cas d’un circuit R-L-C série, la puissance réactive est :

Q est de même signe que.

 

IV- Puissance complexe – Théorème de Boucherot

 

1.      Puissance complexe

Soit u et et la notation complexe de et de.

On a, dans ce cas : et

 

Par définition, on appelle puissance complexe l’expression :

 

 

-          son module est la puissance apparente S ;

-          son argument est le déphasage j ;

-          sa partie réelle est la puissance active  ;

-          sa partie imaginaire est la puissance réactive  ;

De même :

 

2.      Théorème de Boucherot

Considérons un circuit constitué des appareils A₁, A₂, ….., A_n en série. Dans ce cas, on a :

D’où :

Dans le cas des appareils en dérivation, on a :

Et

On a :

La puissance complexe d’un réseau alimenté en courant sinusoïdal est égale à la somme des puissances complexes des appareils qui le constituent.

On a donc :

 

 

Ces relations expriment le théorème de Boucherot :

-          La puissance active totale d’un réseau est la somme des puissances actives partielles ;

-          La puissance réactive totale d’un réseau est la somme algébrique des puissances réactives partielles.

 

 

V-  Facteur de puissance

 

est appelé facteur de puissance, on le note .

Considérations une installation électrique qui alimente un circuit sous une tension et un courant.

-          L’intensité efficace dans la ligne d’alimentation de résistance R est :

-          La puissance perdue par effet Joule est :

 

-          La perte relative dans la ligne est :

 

Cette perte est inversement proportionnelle au carré du facteur de puissance.

Pour réduire cette perte relative k, il faut augmenter le facteur de puissance de l’installation ().

Dans les petites installations, on met en parallèle avec celle-ci un condensateur.

Dans ce cas, la puissance dans le condensateur est entièrement réactive, le courant étant en quadrature avance sur la tension, l’intensité dans la ligne devient :

 

 

 

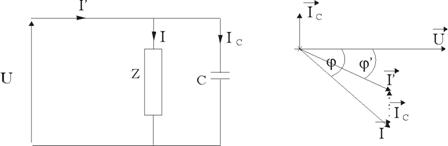
D’après la représentation de Fresnel on a :

 

Le condensateur permet de relever le facteur de puissance de la valeur à la valeur.

Donc

Si (), alors

 

 

 

 

 

I-     Définitions

 

Une installation triphasée est constituée d’un ensemble de trois phases et un neutre.

 

 

 

 

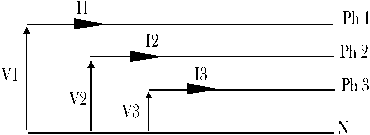
Les tensions v₁, v₂ et v₃ sont déphasées entre elles de 120°, elles s’expriment de la manière suivante :

 

origine des tensions ;

 

Représentation graphique

 

 

 

 

 

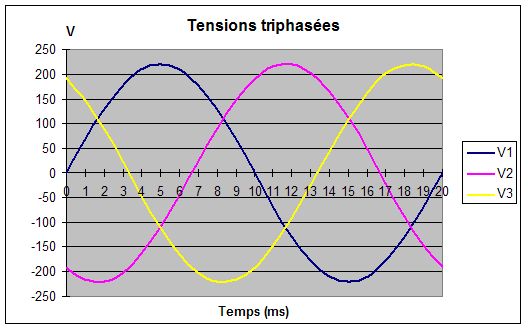
Représentation de Fresnel

 

 

 

 

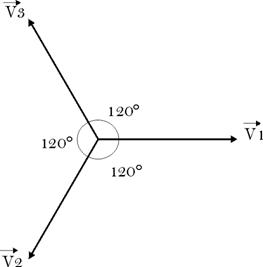
De même le déphasage entre les courants de phases est de 120°.

-                On appelle tension simple la tension entre phase et neutre, on la note V ;

-                On appelle tension composée la tension entre phases, on la note U.

 

On dit qu’un système triphasé est équilibré ou symétrique lorsque les vecteurs qui le composent ont le même module et sont déphasés l’un par rapport à l’autre de 120°.

Si ces conditions ne sont pas remplies, le système est dit déséquilibré.

 

 

II-  Montage étoile et montage triangle

 

1-     Montage étoile :

 

Dans un montage en étoile, les récepteurs (ou bobines génératrices) ont un point commun, c’est le neutre.

 

I : courant de ligne  et J : courant de phase.

 

Relations entre les grandeurs simples et les grandeurs composées :

On a J₁ = I₁, J₂ = I₂ et J₃ = I₃.

 

La tension composée représente la ddp entre deux phases, soit:

 

 

 

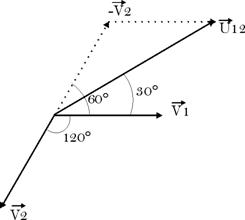
D’après la représentation graphique, on écrit:

 

 ;

D’où 

 

Si V = 220 V, U = 380 V et on note, pour un système triphasé 220/380V.

 

2-     Montage triangle :

 

Dans un montage triangle, les récepteurs sont disposés en triangle de telle sorte d’être soumis aux tensions composées.

 

 

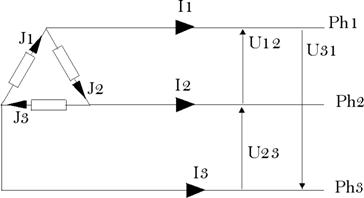
Les tensions composées sont égales et en phase avec les tensions simples (tension simple = tension aux bornes d’un récepteur).

 

On a : U₁₂ = V₁, U₂₃ = V₂ et U₃₁ = V₃ ;

De même :

Dans un système triphasé équilibré, on a :

J₁ = J₂ = J₃ = J et I₁ = I₂ = I₃ = I, le déphasage est de 120°.

 

 

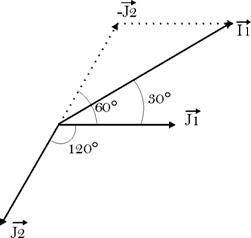
De la même façon on établit la relation entre les courants de phase et ceux de ligne, soit :

 

 

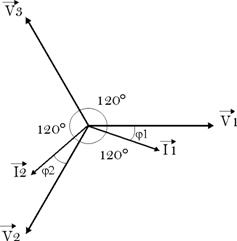
Les courants de ligne sont égaux à fois les courants de phase et déphasés de 30° par rapport à ceux-ci.

 

 

III-          Puissance en système triphasé équilibré

 

1-     Montage étoile :

 

Les récepteurs sont soumis à la tension simple V et traversés par le courant de ligne I ;

 

a.                 Puissance active :

 

P = V₁I₁cos (j₁) + V₂I₂cos (j₂) + V₃I₃cos (j₃)

= 3 VIcos(j) (système équilibré)

Comme, on a :

 

b.                 Puissance réactive :

De la même façon que la puissance active, on établit la relation de la puissance réactive :

 

 

 

2-                 Montage triangle

 

Les récepteurs sont soumis à la tension composée U et parcourus par les courants de phase J ;

 

a.                 Puissance active :

 

P = U₁₂J₁cos (j₁) + U₂₃J₂cos (j₂) + U₃₁J₃cos (j₃)

= 3UJcos (j)

 

Comme, on a :

 

b.                 Puissance réactive :

 

De la même façon que la puissance active, on établit la relation de la puissance réactive :

 

 

 

IV-          Mesure de la puissance en triphasé

 

1-     Mesure de la puissance active

 

Le wattmètre indique le produit du courant efficace par la tension efficace et par le cosinus du déphasage entre cette tension et ce courant.

Autrement dit, la valeur moyenne du produit des valeurs instantanées du courant et de la tension.

Le courant étant l’intensité dans le gros fil du wattmètre et la tension étant la ddp aux bornes du fil fin.

Le schéma équivalent d’un wattmètre est le suivant :

 

 

 

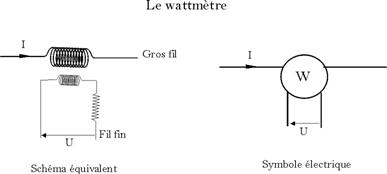
a.                 Système triphasé en étoile avec fil neutre

La puissance active est la somme des puissances consommées par chaque élément (Théorème de Boucherot).

On place donc trois wattmètres de la façon suivante :

 

P = W₁ + W₂ +W₃

Avec: W₁ = V₁I₁ cos j₁, W₂ = V₂I₂ cos j₂ et W₃ = V₃I₃cos j₃

 

Cas d’un système équilibré

V₁ = V₂ = V₃ = V ;

I₁ = I₂ = I₃ = I ;

j₁ = j₂ = j₃ = j ;

D’où: W₁ = W₂ = W₃ = W = VI cos j

 

La puissance totale, d’après le théorème de Boucherot, est :

 

 

b.                 Système triphasé en étoile sans fil neutre

 

 

 

                                                              i.      Système équilibré (utilisation d’un seul wattmètre)

Dans ce cas, il suffit de constituer un point neutre P au même potentiel que le point commun O. Pour cela, on interpose entre les fils de ligne et le point neutre P trois impédances identiques dont l’une est le fil fin du wattmètre.

 

 

On a : P = 3W ;

 

                                                            ii.      Système déséquilibré (utilisation de trois wattmètres)

On constitue un point neutre P, dans ce cas son potentiel est différent de celui de O, son potentiel par rapport à O est noté V.

 

 

 

On a donc :

 

D’après le théorème de Boucherot, on a :

 

P = W₁ + W₂ + W₃

Or le système est couplé en étoile sans fil neutre, c’est-à-dire le courant dans le neutre est nul ().

 

 

Et par conséquent, on trouve :

 

 

Le potentiel du point P est donc éliminé dans le calcul.

 

                                                          iii.      Méthode des deux wattmètres

Dans le cas précédent, et comme le potentiel de P est éliminé dans le calcul, on peut le choisir n’importe où, on le prend sur l’un des fils de phase (3^ème par exemple).

 

 

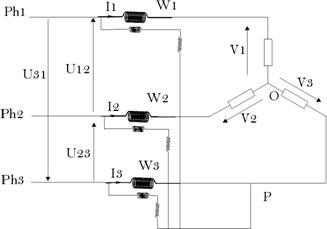
Le wattmètre 3 est donc éliminé et on ne prend en considération que les deux wattmètres 1 et 2.

 

 

Dans ce cas, on a :

 

On se place dans le cas d’un système triphasé équilibré, dans lequel les tensions et les courants sont déphasés entre eux de 120°.

 

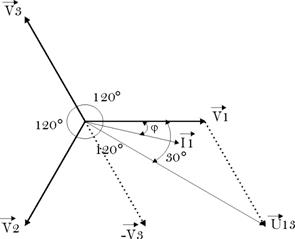
puisque

Donc,

Et par conséquent, on aura :

De même :

 

La puissance totale est donc :

 

 

Remarques :

- Dans le cas d’un système équilibré, on a montré qu’avec un point neutre P quelconque on a, la méthode des deux wattmètres est bien adaptée et d’application courante aux systèmes déséquilibrés.

- Rien ne distingue, sur les fils de ligne, un système en étoile sans fil neutre d’un système en triangle. C’est pourquoi la méthode des deux wattmètres est aussi applicable au système triphasé en triangle.

 

 

 

 

 

Cas particuliers :

·                   j = 0, donc cos (j) = 1 et W1 = W2

Lorsque les indications des deux wattmètres sont égales, le facteur de puissance est égal à 1.

·                   , donc cos (j) = 0,5

o       (le courant est en retard de phase par rapport à la tension)

 

 

o       (le courant est en avance de phase par rapport à la tension)

 

Lorsque l’un des deux wattmètres indique une valeur nulle, le facteur de puissance est égal à 0,5.

 

·                   cos (j) < 0,5

o       , W2 < 0 et W1 > 0

o       , W2 > 0 et W1 < 0

Lorsque les wattmètres indiquent des valeurs opposées, on a :

Remarque :

On peut aussi croiser les connexions de la bobine fil fin (tension) de l’un des deux wattmètres.

 

Détermination du déphasage par la méthode des deux wattmètres dans le cas d’un système équilibré

 

On peut écrire :

 

 

De même :

 

 

La méthode des deux wattmètres est utilisée sur n’importe quelle phase prise comme référence.

 

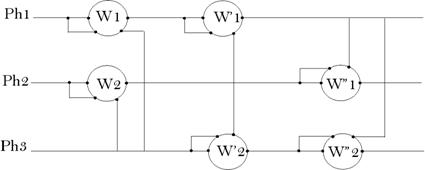
On a toujours :

P = W₁ + W₂ = W’₁ + W’₂ = W’’₁ + W’’₂

 

2-     Mesure de la puissance réactive

 

a.                 Système triphasé équilibré

On monte le wattmètre de la façon suivante :

 

Dans ce cas :

 

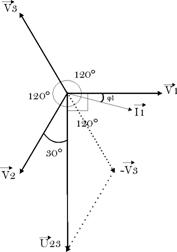
Dans ce cas, on a :  ;

Soit   et

D’où :

 

Remarque :

On peut déduire Q à partir de la méthode des deux wattmètres :

 

 

b.                 Système triphasé déséquilibré

Nous nous plaçons dans le cas le plus fréquent, système déséquilibré en courants mais équilibré en tensions (les tensions composées sont imposées par le générateur supposé à puissance infinie).

 

                                                        i.            Utilisation de trois wattmètres

 

 

 

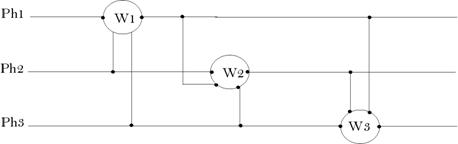
                                                      ii.            Utilisation de deux wattmètres

Dans ce cas, on doit constituer un point neutre, c’est la méthode de ILIOVICI.

Pour cela on utilise trois résistances égales de la façon suivante :

 

 

 

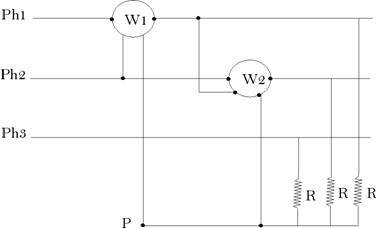
On a vu précédemment que le potentiel de P s’élimine dans le calcul puisque le système est sans fil neutre :

 

Et

 

 

Cas du système équilibré :

et

 

 

Remarque :

W2 est toujours négatif ;

W1 > 0 pour  ;

W1 < 0 pour.

Donc, on additionne les indications des wattmètres pour () et on les retranche pour ().

 

 

 

 

I-     Transformateur parfait :

 

1.      Description :

 

Le transformateur est un convertisseur de tension alternative ou de courant alternatif, il consiste à modifier leur amplitude, en l’abaissant ou en l’élévant, sans pour autant modifier la fréquence.

Le transformateur est constitué de plusieurs enroulements indépendants,(dits primaire et secondaires) et d’un noyau ferromagnétique qui est le siège d’un champ magnétique forcé.

 

 

 

 

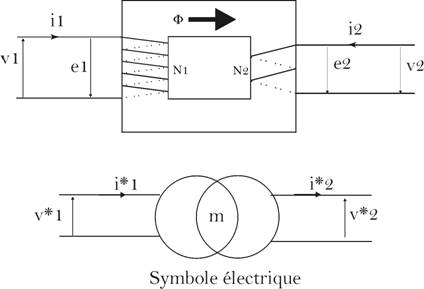
L’application d’une tension alternative aux bornes de l’enroulement primaire fait apparaître une f.e.m induite aux bornes des enroulements secondaires par la circulation d’un flux magnétique à l’intérieur du noyau commun aux deux bobines. Les enroulements secondaires peuvent débiter un courant à travers une charge et le maintenir tant que le primaire reste alimenté par une source alternative.

On dit que le transformateur est un dispositif à flux forcé.

On définit un transformateur idéal comme étant un circuit magnétique fermé de perméabilité infinie, c'est-à-dire, sa réluctance est nulle, le noyau ne présente ni fuites ni pertes ferromagnétiques, et les enroulements ont une résistance nulle.

 

2.      Conventions de signes :

 

Dans le cas du transformateur, on applique, comme pour les bobines, la règle du tire-bouchon, c'est-à-dire :

- Des f.e.m positives apparaissant dans des enroulements tendent à y faire circuler des courants positifs.

- Des courants positifs dans les bobines tendent à créer des flux positifs dans le moyen ferromagnétique.

- La tension et le courant dans le primaire sont liés par la convention des récepteurs.

 

Remarque :

On affectera d’un indice 1, toutes les grandeurs relatives à l’enroulement primaire et d’un indice 2, celles relatives aux enroulements secondaires.

 

3.      Formule de Boucherot :

 

Pour établir la formule de Boucherot, on considère un transformateur parfait dont la section S du noyau ferromagnétique est constante.

On sait que :

(et sont colinéaires)

 

Soit, pour des grandeurs instantanées :

 

 

Si, alors

La f.e.m induite dans l’enroulement est donc :

-    pour une spire :

 

-    pour N spires :

La tension est en quadrature de phase retard par rapport au flux.

Avec :

()

 

D’où,

 

 

Exemple :

, , et

 

 

4.      Représentation complexe des tensions :

 

La f.e.m induite dans une spire par suite d’un flux magnétique variable s’écrit :

 

 

La source est une tension sinusoïdale, qui provoque la création d’un champ magnétique sinusoïdal et par conséquent un flux magnétique sinusoïdal.

En représentation complexe, les grandeurs sinusoïdales s’expriment de la façon suivante :

 

Par conséquent :

o       L’enroulement primaire de N1 spires est le siège d’une f.e.m induite de :

 

o       L’enroulement secondaire de N2 spires est le siège d’une f.e.m induite de :

Puisque les deux enroulements enlacent le même flux magnétique.

 

Et d’après les conventions de signes, on a :

 

et

 

Donc, les expressions complexes des tensions s’écrivent :

Ce qui donne :

Avec est le rapport de transformation du transformateur.

Le signe (-) indique une opposition de phases entre les grandeurs au primaire et aux secondaires.

On distingue différents types de transformateurs selon la valeur du rapport de transformation on a :

- Si, le transformateur fonctionne en élévateur de tension ;

- Si, le transformateur fonctionne en séparateur galvanique ;

- Si, le transformateur fonctionne en abaisseur de tension.

 

 

 

5.      Représentation complexe des intensités.

 

En tenant compte des conventions de signes :

 

 

 

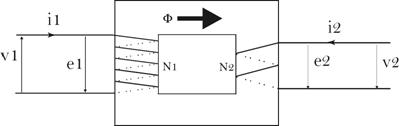
Nous pouvons utiliser la relation d’Hopkinson de la façon suivante :

 

Or, pour un transformateur parfait, dont le noyau ferromagnétique a une perméabilité infinie, donc une réluctance nulle, , il en résulte que :

Et

Le rapport de transformation des intensités est l’inverse de celui des tensions.

 

a. Propriétés du transformateur parfait :

·                     Conservation de la puissance apparente

Nous avons établit que :

 

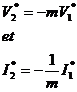
Représentation de Fresnel

 

- et sont en opposition de phase ;

- est déphasé de par rapport à  ;

- et sont en opposition de phase ;

 

 

 

La relation indique qu’il y a conservation de la puissance apparente complexe.

On a donc :

-                      Puissance appelée par le primaire sur la source d’alimentation est :

-                      Puissance fournie à la charge par le secondaire est :

 

La conservation de la puissance apparente conduit aux égalités suivantes :

et

 

·                     Adaptation d’impédance

 

On considère une charge alimentée par le secondaire du transformateur parfait :

 

 

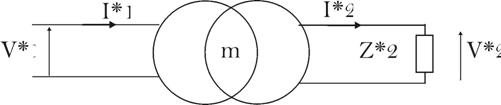
Au secondaire, on a :  ;

Au primaire, on a :

C’est comme si la source alimentait une impédance

est l’impédance équivalente, vue par la source, au transformateur parfait de rapport débitant dans .

Cette propriété nous conduit à la possibilité de ramener au primaire une partie de la charge secondaire, d’un transformateur parfait, en la divisant par.

En effet, considérons le schéma suivant :

 

 

On a : de même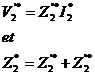

 

L’impédance ramenée au primaire est :

Considérons, maintenant le schéma suivant :

 

 

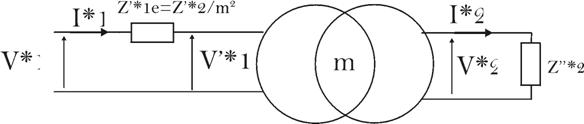
L’impédance vue par le primaire est :

 

 

Les deux schémas sont donc équivalents par la source d’alimentation primaire.

De même, dans les deux cas, la tension aux bornes de est :

(1)

(2)

 

 

 

II-  Transformateur réel

 

Le transformateur réel possède les propriétés suivantes :

- Les enroulements ont des résistances non nulles, ainsi que des pertes de flux (inductance) ;

- Le circuit ferromagnétique est de réluctance non nulle, saturable et présente des pertes fer.

Ceci nous conduit à représenter le transformateur par le schéma équivalent suivant :

 

 

 

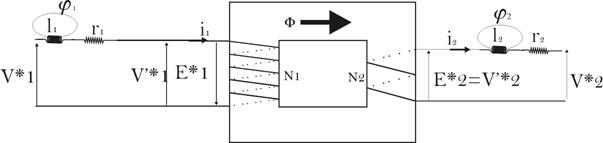
1.      Equations du transformateur réel :

 

a.                                                                                                                                    Loi des mailles appliquée au primaire :

En complexe, on écrit :

 

 

b.                  Loi des mailles appliquée au secondaire :

 

 

Les tensions et représentent ici les tensions primaire et secondaire d’un transformateur parfait.

L’expression du flux peut s’écrire :

 

Soit :

Le flux ne dépend pas seulement de la tension d’alimentation, mais aussi de l’intensité du courant au primaire et de sa phase, donc de la charge du transformateur.

De façon générale, la chute de tension (vectorielle) au primaire est négligeable devant la tension d’alimentation, on écrit alors :

 

Soit :

On considère donc que le transformateur réel est un dispositif à flux forcé (imposé par la tension d’alimentation au primaire).

Ceci nous conduit à la formule de Boucherot, dans le cas d’un transformateur parfait :

 

 

La relation d’Hopkinson appliquée au circuit magnétique permet d’écrire :

 

 

 

 

Le flux magnétique est imposé par, on peut encore écrire :

 

En fonctionnement à vide () du transformateur alimenté par la même tension, le courant au primaire est.

Or, la force magnétomotrice est la même car le flux est identique (flux forcé), ce qui s’exprime par :

 

 

2)     Schéma équivalent d’un transformateur réel :

 

En tenant compte des relations établies précédemment,

 

D’où :

On peut considérer le transformateur parfait de tensions primaire et secondaire et et de rapport.

Les intensités au primaire et au secondaire sont et.

Ceci explique que l’intensité au primaire du transformateur diffère de celle dans, cette différence résulte d’une dérivation aux bornes du transformateur, dans laquelle circule le courant.

On représente cette dérivation par une inductance pure consommant le courant magnétisant (partie imaginaire de, courant réactif) en parallèle avec une résistance consommant le courant actif (partie réelle de).

Ce qui nous conduit au schéma complet de transformateur réel :

 

 

 

 

3)     Schéma électrique simplifié :

 

Afin de simplifier les calculs, on ramène l’impédance du secondaire au primaire (en divisant par), ce qui devient :

 

 

 

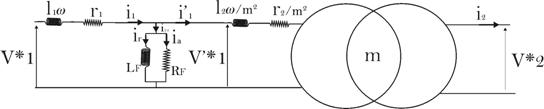
C’est le schéma en T.

 

Tous les éléments associés aux pertes du transformateur réel sont rassemblés au primaire sous forme d’un quadripôle en T.

 

4)     Séparation des pertes des enroulements et du circuit :

 

Sachant que la chute de tension aux bornes de est faible devant et que est faible de (), on peut écrire :

, ()

Ce qui revient à placer, sans erreur sensible, la bobine (L_1F//R_1F) en amont de.

Le schéma en T devient G.

 

 

 

 

Cette impédance rassemble toutes les pertes des enroulements (effet Joule et fuites de flux), ramenées au primaire.

Cette impédance peut être ramenée au secondaire, on aura donc :

 

 

Avec :

 

 

5)     Hypothèse simplifiée de Kapp :

 

En admettant que est négligeable devant (nominal), on peut simplifier encore le schéma électrique en remplaçant la bobine fictive magnétisante par un circuit ouvert (la supprimer), ceci n’a pas de conséquence sensible sur le courant primaire.

Le schéma devient :

 

 

Impédances ramenées au primaire.

 

 

 

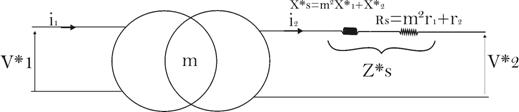
Impédances ramenées au secondaire.

 

et représentent les impédances totales des pertes des enroulements ramenées au primaire ou au secondaire.

 

6)     Représentation de Fresnel selon l’approximation de Kapp :

 

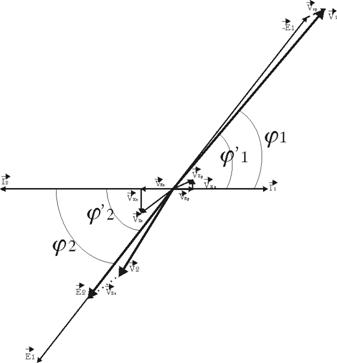
Reprenons le schéma réel :

 

 

On a :

·         et sont en opposition de phase :  ;

·         et sont en phase :  ;

·         est en retard de phase de par rapport à  ;

·         est en retard de phase de par rapport à.

 

 

 

 

 

 

 

III-          Transformateur en charge

 

Sur la plaque signalétique d’un transformateur on indique :

-          la tension primaire  ;

-          la fréquence ;

-          la tension secondaire à vide  ;

-          la puissance apparente S ;

-          parfois la tension de court-circuit en pourcentage.

 

1.      Caractéristiques d’un transformateur :

 

a.                                                                                                                                    Courbes  : ce sont les caractéristiques en charge du transformateur, elles se tracent à facteur de puissance constant.

On sait que :

 

 

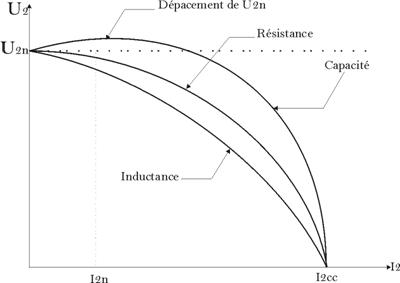
La tension aux bornes d’une charge capacitive peut, dans certains cas, dépasser la tension à vide.

 

b. Chute de tension

o       Valeur absolue : c’est la différence entre les valeurs efficaces de la tension secondaire à vide et en charge :

 

o       Valeur relative : elle exprime en pourcentage la qualité du transformateur, elle est définie par :

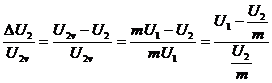
Un bon transformateur a une chute de tension relative inférieure à 4% pour le courant secondaire nominal.

o       Détermination de la chute de tension par la méthode de Kapp :

D’après l’hypothèse de Kapp, on peut faire la représentation de Fresnel des grandeurs électriques au secondaire du transformateur ;

 

 

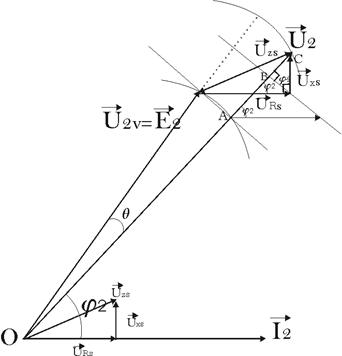
Dans ces conditions, on peut écrire, compte tenu de la valeur faible de q :

 

De même, est la chute de tension au secondaire du transformateur.

D’où

 

 

c. Tension de court-circuit

Dans un transformateur en court-circuit avec une tension primaire nominale, l’intensité du courant secondaire est tellement élevée qu’elle puisse rendre le transformateur inutilisable (rupture ou échauffement de l’enroulement). C’est pourquoi un transformateur en court-circuit ne peut être utilisé que sous une tension réduite.

Définition : On appelle tension de court-circuit nominale d’un transformateur, la tension (réduite) qu’il faut appliquer au primaire pour obtenir dans le secondaire en court-circuit un courant égal au courant nominal.

Elle s’exprime en % de tension nominale.

 

2.      Rendement du transformateur :

 

a.                                                                                                                                    Définition :

C’est le rapport des puissances actives du secondaire et du primaire.

On dit aussi que est la puissance absorbée, , et est la puissance utile .

 

b. Bilan des pertes :

·               Pertes dans le fer ()

Elles sont dues à l’hystérésis et aux courants de Foucault.

 

et sont des coefficients, est le volume en .

 

Ces pertes ne dépendent que du champ maximalet de la fréquence.

Pour une fréquence constante, le champ est sensiblement invariable à toute charge puisque la tension primaire est constante (imposée).

Les pertes dans le fer sont donc indépendantes de la charge :

·               Pertes dans le cuivre ()

Ce sont les pertes par effet Joule dues aux résistances des enroulements :

Comme

Alors :

 

Les pertes dans le cuivre sont proportionnelles au carré de l’intensité du courant secondaire.

 

 

·               Expression du rendement

 

Sachant que :

 

Le rendement s’écrit donc :

 

 

 

 

c. Maximum du rendement pour et constants :

On peut écrire :

est sensiblement constante pour un facteur de puissance donné, donc est constant et le rendement est maximal lorsque le dénominateur est minimal, c’est-à-dire, la somme est minimale. Ceci est obtenu lorsque.

Le rendement d’un transformateur est maximal quand ses pertes dans le cuivre sont égales à ses pertes dans le fer.

 

d. Maximum du rendement pour et constants :

On peut écrire :

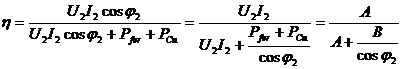
est maximal lorsque . C’est le cas d’une charge purement résistive.

 

 

3.      Détermination pratique du rendement :

 

a. Essai à vide : le transformateur est alimenté sous une tension primaire nominale.

Montage :

 

 

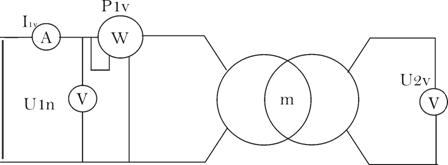
Or, puisque  ;

De même est très faible.

D’où,

b. Essai en court-circuit : le transformateur est alimenté sous une tension primaire réduite, le champ est donc réduit et par conséquent, les pertes dans le fer deviennent presque nulles. On peut admettre qu’en court-circuit, il n’y a pratiquement pas de pertes dans le fer,.

 

 

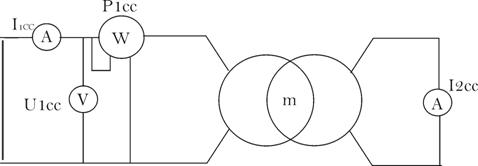
De même, , du fait que .

Soit,

 

Quand le transformateur débitera un courant dans une charge, les pertes dans le cuivre auront la même valeur que dans l’essai en court-circuit pour ce même courant.

 

Pour une valeur quelconque du courant de charge, on a :

Et

 

 

 

 

 

 

I.       Constitution des transformateurs triphasés

 

1.      Présentation

 

                                                              i.      L’utilisation d’un transformateur monophasé sur une phase d’un système triphasé est possible, et par conséquent, l’association de trois transformateurs monophasés, chacun sur une phase, est aussi possible.

Toutefois, l’utilisation d’un seul transformateur, dit triphasé, avec trois enroulements primaires et trois enroulements (ou plus) secondaires fait gagner en encombrement et en poids de fer utilisé.

 

                                                            ii.      Avec des tensions équilibrées, on devrait avoir des flux équilibrés, ce qui exigerait une disposition des noyaux portant les enroulements de type étoile ou triangle.

 

 

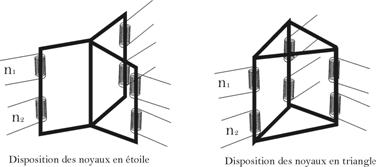
                                                          iii.      En pratique, on réalise des transformateurs à noyaux coplanaires. Sur chaque noyau se trouvent un enroulement primaire et un enroulement secondaire soigneusement isolés l’un de l’autre.

 

 

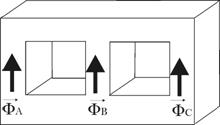
Dans cette disposition, les flux dans les enroulements sont dépendants entre eux, on a la contrainte :

On dit qu’un tel transformateur est à « flux lié ».

 

Pour remédier à ce problème de dépendance et pour que les flux dans les trois enroulements soient indépendants, on ajoute quelques fois des noyaux latéraux.

 

 

On dit que le transformateur est à flux libre, dans ce cas le flux s’écrit :

 

2.      Les enroulements

 

                                                              i.      Mode de connexion :

Les enroulements d’un transformateur triphasé (primaires et secondaires) peuvent être couplés en étoile ou en triangle, comme les récepteurs en système triphasé.

Une troisième configuration peut être attribuée au secondaire, il s’agit du couplage en zig-zag : un enroulement secondaire se trouve sur deux noyaux différents et correspond ainsi à deux enroulements primaires appartenant à deux phases différentes.

Ce type de couplage permet de mieux répartir le déséquilibre, si déséquilibre il y a, entre les trois phases du primaire.

 

 

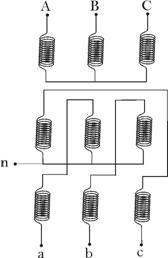
                                                            ii.      Représentation symbolique des couplages :

Avec ces différents couplages, étoile et triangle au primaire et étoile, triangle et zig-zag au secondaire on obtient les combinaisons suivantes :

On note : Y pour étoile, D (ou D) pour triangle et Z pour zig-zag.

Soit un ensemble de six combinaisons possibles : YY, YD, YZ, DY, DD et DZ.

Une représentation plus significative consiste à utiliser une lettre majuscule pour la haute tension et une lettre minuscule pour la basse tension.

 

 

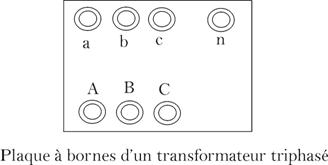
                                                          iii.      Repérage des bornes :

Elles sont repérées par les lettres A,B et C côté haute tension et a, b et c pour les phases correspondantes de la basse tension.

S’il y a un neutre (cas de Y ou Z), on ajoute la lettre N ou n à la borne correspondante.

 

 

II.    Equations électriques d’un transformateur triphasé

 

 

1.      Equation d’une colonne :

 

Chaque colonne du transformateur triphasé se comporte comme un transformateur monophasé dont l’équation des tensions s’écrit :

 

 

Et

En tenant compte des représentations triphasées, on écrit :

 

 

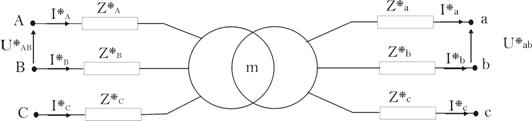
De même, en tenant compte des approximations faites dans le cas du transformateur monophasé, on peut écrire :

et

 

La description du transformateur triphasé sera donc basée sur les trois transformateurs colonnes (monophasés) et l’ensemble de leurs diagrammes vectoriels associés.

Il suffit de représenter les diagrammes vectoriels d’une colonne et d’en déduire les autres par rotation de 120°.

 

2.      Grandeurs caractéristiques d’un T.T

 

                                                              i.      Fonctionnement nominal :

Sur la plaque signalétique d’un transformateur triphasé, on indique :

-          la puissance apparente utile  ;

-          les tensions primaire et secondaire composées, entre fils de ligne. Si le mode de connexion n’est pas fixé, on indiquera les valeurs nominales des tensions correspondantes à chaque couple possible.

Exemple :

Si une plaque porte les indications suivantes :

o       primaire :

§         étoile :  ;

§         triangle :  ;

o       secondaire :

§         étoile :  ;

§         triangle :

cela signifie que les enroulements sont prévus pour travailler sous les tensions normales suivantes :

§         primaire :  ;

§         secondaire :

Les intensités des courants secondaires en ligne :

-          La valeur du facteur de puissance de la charge qui permet d’obtenir le fonctionnement nominal (tensions primaire et secondaire nominales, puissance utile nominale).

 

 

                                                            ii.      Rapport de transformation

C’est le rapport des tensions secondaire et primaire de même définition (toutes les deux l ou toutes les deux D) :

 

                                                          iii.      Indice horaire

-          Convention de repérage :

On considère que les enroulements d’un transformateur monophasé sont situés sur la même colonne et enroulés de la même façon.

 

 

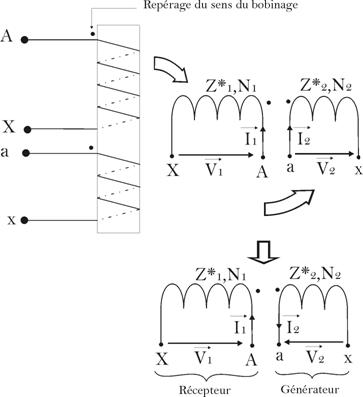
Dans cette configuration, on a :

 

et

De même : et

Ceci conduit à l’expression, établie précédemment :

 

 

-          Indice horaire :

 

 

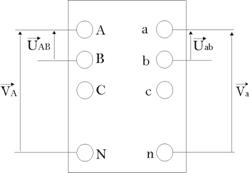
Si le primaire du transformateur est soumis à un système triphasé équilibré, le secondaire délivrera un système triphasé équilibré. Toutefois, un déphasage q est introduit entre les tensions homologues primaires et secondaires, entre et, et, et, de même entre et, et, et.

Ce déphasage q est une caractéristique du transformateur triphasé.

 

 

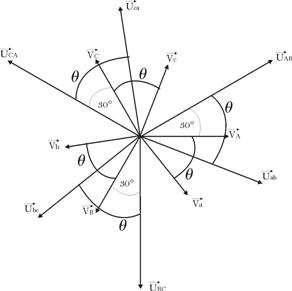
En pratique, les valeurs de q obtenues sont toujours des multiples de. On indiquera donc le rapport de q à  :

Ce nombre est appelé indice horaire du transformateur, il est compris entre 0 et 11.

 

Un déphasage de q = 90° correspondrait à un indice horaire I = 3.

 

Remarque :

L’indice I et l’angle q caractérisent le retard d’une tension basse BT sur son homologue haute HT quelque soit le transformateur, abaisseur ou élévateur.

 

 

III. Couplages du transformateur triphasé

 

1.      principe

 

Les enroulements primaires peuvent être couplés en étoile ou en triangle, les enroulements secondaires, eux, peuvent être couplés en étoile, triangle ou zig-zag.

 

 

 

 

Le mode de couplage est choisi selon un certain nombre de critères :

                                                              i.      fonctionnement nominal

·         pour les très hautes tensions, il importe de choisir un couplage étoile, pour que l’enroulement ne supporte que  ;

·         pour les intensités importantes, un couplage en triangle est recommandé, le courant dans l’enroulement est  ;

                                                            ii.      incidence et déséquilibre

Les couplages en triangle sont à éviter dans le cas des sources triphasées, à moins de disposer de protections très efficaces.

(S’assurer que est toujours vérifiée,).

De façon générale, on évitera le couplage triangle au secondaire.

 

                                                          iii.      fonctionnement déséquilibré

·         aux faibles déséquilibres (), primaire et secondaire seront couplés en étoile avec fils neutres ;

·         si le déséquilibre est plus important, le primaire sera couplé en étoile et le secondaire en zig-zag ;

·         si le déséquilibre et la puissance sont importants, le primaire sera couplé en triangle et le secondaire en étoile, pour minimiser l’effet Joule.

                                                          iv.      Marche en parallèle

L’installation des transformateurs triphasés pour un fonctionnement en parallèle, impose qu’ils aient le même indice horaire (et pas nécessairement le même couplage).

 

2.      Couplages normalisés

 

                                                              i.      Couplage étoile-étoile (Yy)

Equation aux tensions :

 

 

 

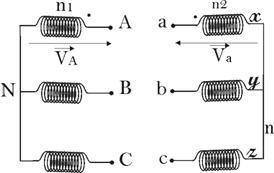
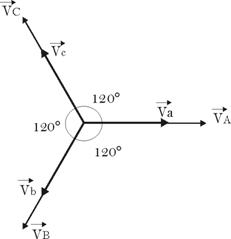
Rapport de transformation :

et sont en phase (q = 0 et I = 0).

On désigne ce couplage par Yy0 (Haute Tension, Basse Tension, Indice horaire).

 

                                                            ii.      Couplage triangle-étoile (Dy)

 

 

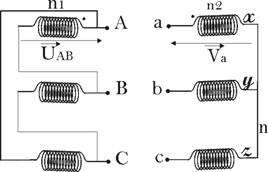
Equation aux tensions:

 

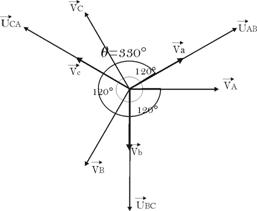
Dans ce cas, q = 330° et I = 11.

 

Rapport de transformation :

Ce couplage sera désigné par Dy11.

 

                                                          iii.      Couplage étoile-zig-zag (Yz)

Dans ce cas, le secondaire comporte deux enroulements identiques.

 

 

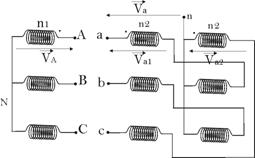
Equation aux tensions :

Donc, q = 330° et I = 11.

 

Désignation : Yz11.

 

Rapport de transformation :

 

 

IV.Utilisation du transformateur triphasé

 

1.      Essai à vide

 

Le couplage est alimenté sous tension nominale, on mesure donc : , , et .

Ces valeurs permettent de donner les pertes dans le fer et le rapport de transformation.

Ces mesures peuvent être faites pour une colonne et généralisées au transformateur triphasé, dans le cas d’un système équilibré. Ou bien on utilise un wattmètre triphasé.

Détermination des pertes dans le fer :

cas d’un couplage étoile ;

cas d’un couplage triangle ;

 

Remarque : De façon générale, on néglige les pertes par effet Joule à vide devant la puissance à vide.

 

2.      Essai en court-circuit

 

On doit réaliser un court-circuit symétrique avec trois ampèremètres montés en étoile, ou bien avoir un court-circuit franc et calculer le courant en mesurant.

La puissance en court-circuit représente, aux pertes fer près, les pertes par effet Joule, .

On en déduit :

-          impédance :

 

-          résistance :

-          réactance :

-          facteur de puissance en CC :

 

3.      Rendement du transformateur

 

Le rendement d’un transformateur est donné par le rapport des puissances utile et absorbée (secondaire et primaire) :