Machine Synchrone

Introduction

Le terme de machine synchrone regroupe toutes les machines dont la vitesse de rotation de l’arbre de sortie est égale à la vitesse de rotation du champ tournant.

Pour obtenir un tel fonctionnement, le champ magnétique rotorique est généré soit par des aimants, soit par un circuit d’excitation. La position du champ magnétique rotorique est alors fixe par rapport au rotor, ce qui impose en fonctionnement normal une vitesse de rotation identique entre le rotor et le champ tournant statorique.

Cette famille de machine regroupe en fait plusieurs sous familles, qui vont de l’alternateur de plusieurs centaines de mégawatts au moteur de quelques watts, en passant par les moteurs pas à pas.

Néanmoins, la structure de toutes ces machines est relativement proche. Le stator est généralement constitué de trois enroulements triphasés répartis, tel que les forces électromotrices générées par la rotation du champ rotorique soient sinusoïdales où trapézoïdales.

Les stators, notamment en forte puissance, sont identiques à ceux d’une machine asynchrone.

Il existe trois grandes familles de rotor, ayant pour rôle de générer le champ d’induction rotorique:

les rotors bobinés à pôles lisses;

les rotors bobinés à pôles saillants;

les rotors à aimants.

Constitution

Le stator est un bobinage polyphasé (en général branché en Y), qui engendre un champ tournant.

Pour les petites puissances (usuellement < 10 kW), le rotor est à aimants permanents. N'ayant ni collecteur ni balais, le moteur est appelé "brushless".

Pour des puissances plus importantes, le rotor est bobiné. Son alimentation en courant continu

(connexions du + et du –) peut être assurée par un collecteur à deux bagues (beaucoup plus simple que celui d'une MCC).

Il est aussi possible d'associer sur le même arbre une deuxième MS fonctionnant en alternateur, à aimants permanents, de puissance inférieure, débitant dans un pont redresseur tournant qui alimente le rotor de la machine principale. Il n'y a alors ni bagues, ni balais.

Symboles

Modes de fonctionnement

La machine synchrone est réversible, elle peut fonctionner aussi bien en moteur qu'en générateur.

De même, elle peut être de type inductif ou capacitif selon l'excitation.

Fonctionnement dans les quatre quadrants:

Une des particularités de la machine synchrone est sa capacité à fonctionner dans les quatre quadrants électriques. Il est en effet possible de rendre à volonté la machine inductive ou capacitive, que ce soit en fonctionnement moteur ou générateur. Il suffit pour cela de jouer sur l’amplitude de E, c’est à dire sur le courant d’excitation rotorique. On obtient alors les diagrammes de Behn-Eschenbourg suivants :

Il est possible de constater que lors d’un fonctionnement capacitif, la f.e.m. E est supérieure à la

tension d’alimentation, on dit que la machine est surexcitée. Lors d’un fonctionnement inductif, la f.e.m. E est inférieure à la tension d’alimentation, on dit que la machine est sous-excitée.

Fonctionnement en alternateur P<0:

Pour fonctionner en alternateur, l'inducteur (rotor) doit être entraîné mécaniquement en rotation. L'enroulement induit (stator) est alors le siège d'une f.e.m induite quasi sinusoïdale

Cette f.e.m est due à:

Modèle électrique équivalent

Pour étudier l'alternateur triphasé, on modélise l'une de ses phases par une f.e.m. E_PN en série avec une résistance R et une réactance synchrone X = Lw.

E_PN : fem induite à vide;

I : courant de ligne

V : tension entre phase et neutre

r : résistance d'un enroulement statorique (couplage Y)

X = Lw : réactance synchrone d'un enroulement statorique

• Remarques

X est proportionnelle à la vitesse de rotation. Elle tient compte de la réactance réelle de l'enroulement et de la réaction magnétique d'induit.

En pratique X >> r

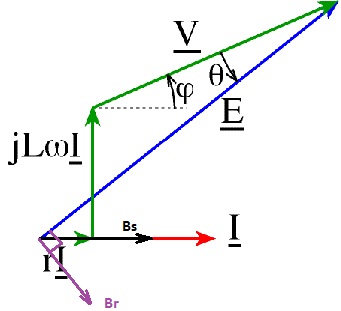
Représentation vectorielle : diagramme de Behn-Eschenburg

C'est la représentation vectorielle des grandeurs électriques.

Loi des mailles avec les grandeurs complexes :

E = V + jLwI + RI

Il peut être utile de connaître deux angles :

• le déphasage j entre le courant et la tension. j et I

varient en fonction de la consommation ;

· le décalage interne q entre V et E.

Remarque : le diagramme ci-dessus est en fait le plus simple pour une machine à pôles lisses et non saturée.

On sait que :

D'où

_{De même, , puisque Bs = aIs.}

_{Ce qui nous permet de faire la représentation suivante:}

F.e.m efficace par enroulement statorique, à vide :

Un enroulement a N conducteurs, soit N/2 spires. Soit F₀ le flux sous un pôle à travers une spire

(Û F = NF₀/2).

L'alternateur fournit par enroulement la tension à vide suivante :

En pratique le "coefficient de Kapp" K_app est propre à chaque type de machine et vaut entre 2,2 et 2,6.

Bilan des puissances d’un alternateur

Puissance absorbée

La puissance absorbée est mécanique :

W_S : pulsation de rotation en rad.s^-1

n_S : vitesse en trs.s^-1

T_M : couple utile sur l’arbre en N.m

Si l’alternateur n’est pas auto-excité il faut encore tenir compte de l’énergie électrique absorbée par l’excitation (rotor).

Puissance utile

En triphasé avec une charge équilibrée de facteur de

puissance cos j:

Bilan des pertes

Pertes par effet joule dans l’inducteur :

Pertes par effet joule dans l’induit :

Où R est la résistance vue entre deux bornes de l’alternateur. Ces pertes dépendent de la charge.

Pertes dites « collectives » pc :

pertes mécaniques et pertes fer qui ne dépendent pas de la charge.

Rendement

ou

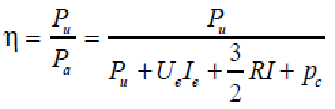
Caractéristiques de l’alternateur synchrone

Caractéristique interne

La caractéristique interne d’un alternateur est la courbe de la force électromotrice E en fonction du courant inducteur i.

E s’obtient par une mesure à vide.

Il s’agit alors de la caractéristique V (i) effectuée :

• à vitesse ou fréquence de rotation n_s constante ;

• à courant induit d’intensité nulle I = 0.

L’alternateur sera utilisé loin de la saturation, c’est à dire dans la région où la courbe E(i) est linéaire.

Remarquons qu’il existe une force électromotrice non-nulle relevée pour i = 0 : elle est due au champ rémanent des pôles.

Caractéristique en court-circuit

La caractéristique en court-circuit est la courbe Icc(i) des variations de l’intensité efficace du courant de court-circuit en fonction de l’intensité i du courant d’excitation tracée:

– à vitesse de rotation ns constante ;

• à tension V = 0.

On observe que l’intensité de court-circuit Icc est proportionnelle à i. Ce sera toujours le cas dans un alternateur synchrone.

L’intensité du courant de court-circuit est proportionnelle au courant d’excitation.

Caractéristique externe

La caractéristique externe est une caractéristique en charge de l’alternateur. Elle est réalisée à l’aide d’une charge d’impédance variable mais de cos j constant. C’est donc la courbe V (I) (ou U(I) selon les cas) :

– à vitesse de rotation ns constante ;

– à courant d’excitation d’intensité i constante ;

• avec une charge dont le facteur de puissance cos j est constant.

Fonctionnement en moteur P>0:

Le moteur synchrone convertit la puissance électrique en puissance mécanique.

Pendant longtemps, ce moteur fût relativement peu utilisé en raison de sa difficulté à réguler sa vitesse. Ce problème est maintenant résolu grâce au progrès de l'électronique de puissance et des onduleurs qui lui sont associés.

Le stator de la machine est alimenté en triphasé ; il se crée alors un champ magnétique tournant à la

fréquence de rotation n=f/p, ce qui fait que le rotor de la machine tourne lui aussi à la fréquence de rotation n.

Comme pour l'alternateur, on modélise une phase du moteur par les éléments E_PN, R, X et V.

Modèle d'une phase d'un moteur synchrone :

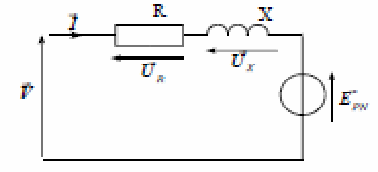
La relation entre les différentes tensions est :

avec :

souvent négligeable.

Et

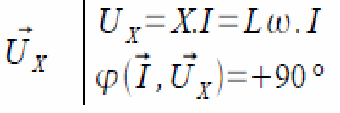
Rendement d'un moteur synchrone :

La puissance fournie est électrique.

Le rendement d'un moteur synchrone est:

Exercices :

Énoncé 1 :

Une machine synchrone monophasée à 6 pôles fonctionne en moteur synchrone . La résistance de l’induit est négligeable et la réactance constante est égale à 8 . On applique aux bornes du moteur une tension de 200 V, fréquence 50 Hz. On règle l’excitation du moteur pour que son facteur de puissance soit égal à 1. Le moteur développe une puissance de 5 kW.

1. On demande :

   1. la vitesse du moteur en tours par minute;

   2. le courant fourni par le réseau;

   3. le couple moteur;

   4. la force contre-électromotrice du moteur.

2. On augmente l’excitation du moteur jusqu’à ce que le facteur de puissance devienne égal à 0,8 , la puissance développée par le moteur reste la même. Déterminer :

   1. le déphasage du courant sur la tension et le sens de ce déphasage;

   2. le courant absorbé par le moteur;

   3. la force contre-électromotrice du moteur.

3. Déterminer graphiquement quelques points du graphe I = f(E) qui donne le courant fourni par le réseau en fonction de la force contre-électromotrice du moteur quand celui-ci développe une puissance de 4 kW. Ces points seront choisis de façon à donner une idée générale de l’allure du graphe. Échelle : 1 mm pour 2 V. On admettra que la puissance fournie par le réseau est intégralement transmise à la roue polaire.

Corrigé :

La vitesse du moteur (en tr/min), compte tenu de la fréquence et du nombre de pôles, est :

1. La puissance développée par le moteur est la puissance absorbée :

   Sachant que ,

2. On admet que la puissance fournie par le réseau est intégralement transmise à la roue polaire (3), d'où :

3. Force contre-électromotrice (ou électromotrice) : , sachant que

   soit :

   

1. On augmente l'excitation, la machine est sur-excitée, le facteur de puissance atteint 0,8.

   

   1. Le déphasage est donc avant, il est de 36,8° (est retard par rapport à ).

   2. La valeur de l'intensité du courant, puissance inchangée, est :

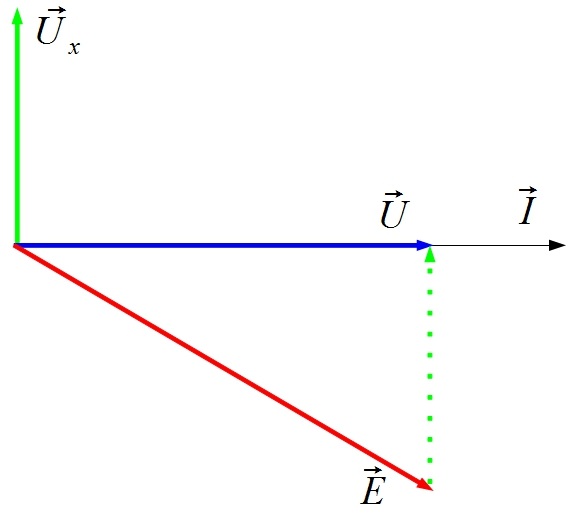
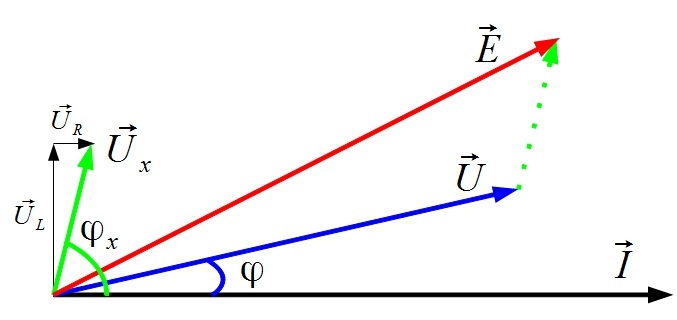
   3. La force contre-électromotrice peut être calculée à partir du diagramme vectoriel :

      sachant que

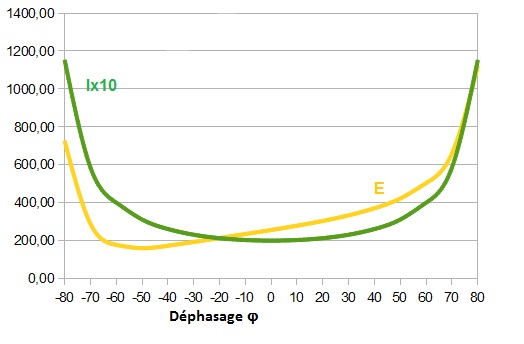
2. Allure de la courbe I=f(E), on fait varier l'excitation, donc le facteur de puissance :

Expression de I :

Expression de E :

Déphasage	-80	-70	-60	-50	-40	-30	-20	-10	0	10	20	30	40	50	60	70	80
I	115,18	58,48	40,00	31,11	26,11	23,09	21,28	20,31	20,00	20,31	21,28	23,09	26,11	31,11	40,00	58,48	115,18
E	725,27	288,11	177,62	160,27	172,98	192,83	213,77	234,76	256,12	278,71	303,79	333,29	370,58	422,17	503,24	659,31	1118,90

Énoncé 2 :

On considère un alternateur monophasé (circuit magnétique non saturé), ayant les caractéristiques suivantes :
- Tension d'induit U = 380 V;
- Fréquence f = 60 Hz;
- Vitesse de rotation N = 900 tr/min;
- Résistance d'induit r = 0,02 

Lorsque le courant d'excitation vaut 9 A, la tension à vide est égale à 420 V. De plus, pour un courant d'excitation de 5 A, l'alternateur débite un courant de court-circuit de 307 A.

1. Déterminer le nombre de pôles de l'alternateur ;

2. Détermination de la réactance synchrone par le diagramme de Behn-Eshenburg ;

3. Le facteur de puissance de l'installation étant de 0,9, trouver la f.é.m. nécessaire pour alimenter le réseau sous une tension U = 380 V, l'alternateur débitant un courant I = 120 A ;

4. En déduire le courant d'excitation correspondant (on considère que la courbe E(i) est linéaire entre 380 et 450 V) ;

Le rotor consomme un courant de i = 5 A sous une tension de 17 V, et les pertes constantes sont égales à 700 W.

5. Calculer pour les conditions des questions 3) et 4), la puissance utile ainsi que le rendement.

Corrigé :

1. Nombre de pôles : , la machine possède 8 pôles.

2. Réactance synchrone :

   Le circuit magnétique est non saturé, la f.e.m est proportionnelle au courant d'excitation :

   

   

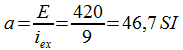
3. Alimentation du réseau :

   

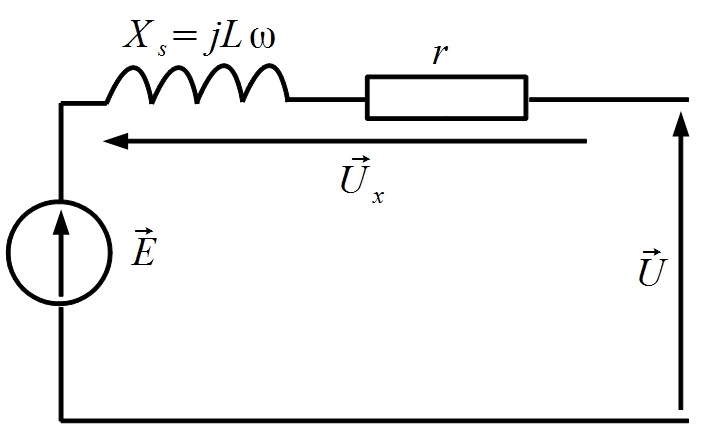
   On a : avec , et

   DE même : et

   D'où :

4. Courant d'excitation :

   La courbe est linéaire entre 380V et 450 V.

5. Puissance utile :

   Rendement :

Énoncé 3 :

Compensateur synchrone :

Les compteurs d’énergie active et réactive installés sur le tableau d’alimentation d’une usine indiquent respectivement 13750 kWh et 16500 kVARh pour une journée.

1. Quel est le facteur de puissance moyen de cette usine ?

2. On veut relever jusqu’à 0,85 le facteur de puissance moyen par l’emploi d’une machine synchrone surexcitée (compensateur synchrone) fonctionnant à vide.

   Si on néglige en première approximation la puissance active absorbée par cette machine, quelle devra être la puissance apparente ?

3. En supposant que la machine considérée absorbe une puissance active égale à 6,5 % de sa puissance réactive, quelle est exactement la puissance apparente du compensateur synchrone à installer ?

Corrigé :

1. Facteur de puissance moyen : 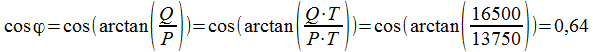, où T représenté une journée (24 h).

2. Le compensateur doit apporter la puissance réactive nécessaire pour relever le facteur de puissance à 0,85.

   Cette puissance est donnée par le bilan suivant :

   La puissance apparente de la machine est donc (P_M = 0) : S_M = Q_M = 332,4 kVA.

3. La machine absorbe 6,5% de sa puissance réactive :

   Un bilan de puissances nous donne : et

   De même, et

   Soit : et

   La puissance apparente de la machine, dans ce cas, vaut :

   
   
   
   
   

   Source: http://meteosat.pessac.free.fr/Cd_elect/ima/DOC_ETT/Pages1a10_de_msyn.pdf