Moteur à excitation séparée

Introduction

Précautions à prendre :

L’alimentation du circuit inducteur doit précéder celle du circuit induit;

La mise sous tension de l’induit doit être progressive;

La machine fonctionne, dans ce cas, en récepteur = moteur;

Elle convertit, donc, l’énergie électrique, qu’elle reçoit, en énergie mécanique (à des pertes près).

Schéma électrique

Le circuit inducteur et le circuit induit sont alimentés séparément: excitation séparée;

L’induit du moteur peut être remplacé par son schéma équivalent:

- R est la résistance de l’induit;

- E est la f.e.m de la machine;

La loi d’Ohm permet d’écrire: U = E + RI

Fonctionnement du moteur

A vide:

Un moteur est dit fonctionnant à vide lorsqu’il n’entraîne aucune charge sur son arbre.

On affectera d’un indice « 0 » les grandeurs mises en jeu.

- I₀ est l’intensité du courant absorbée par l’induit à vide;

- N₀ (trs/min), n₀ (trs/s) et ₀ (rd/s) est la vitesse de rotation à vide, elle est légèrement supérieure à sa valeur nominale.

- U₀ est la tension appliquée à l’induit, le moteur étant à vide.

Elle est réglée à sa valeur nominale.

Force électromotrice:

Dans un moteur en rotation, les conducteurs coupent le flux inducteur exactement dans les mêmes conditions que dans le fonctionnement en génératrice.

La f.e.m est donnée par la même formule quelque soit le mode de fonctionnement:

E = nN

Remarque: On note aussi E’ pour un moteur.

Loi d’Ohm:

Fonctionnement en récepteur:

U = E + R.I

Vitesse de rotation:

D’après les deux formules précédentes, on écrit:

n en trs/s

Réglage de la vitesse:

Dans une machine, R et N sont fixés lors de la construction.

A vide l’intensité I₀ dans l’induit est très faible, soit:

R.I₀ << U et E # U

Dans la pratique, on écrit:

Si U = cte, le flux reste la seule grandeur variable et la vitesse de rotation lui est inversement proportionnelle.

Cette dernière pourra être modifiée en faisant varier l’intensité i du courant d’excitation.

Caractéristique de la vitesse de rotation à vide:

C’est la courbe n(i) ou (i) tracée à U = cte.

On a:

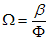
D’où,

Puissance électrique utile P_eu:

Dans le cas d’une machine bipolaire, il y a deux voies d’enroulement, chaque conducteur est traversé par le courant I’=I/2;

En effectuant un demi tour, il coupe la totalité du flux  sous un pôle.

Le travail W=I’=I/2 est effectué en une durée t=1/2n

La puissance développée est donc:

P = W/t=In

La puissance développée par les N conducteurs est alors:

P = NnI

C’est la puissance électrique utile P_eu.

C’est cette puissance qui est transformée en puissance mécanique par le moteur.

Sachant que :

E = Nn

On écrit:

Peu = nNI = E.I

n en trs/s

I en A

 en Wb

E en V

P en W

Moment du couple :

Sachant que :

P =( en rd/s)

et dans ce cas P = P_eu

On écrit:

T = P_eu/ = E.I/ = nNI

=2n

T = NI/2

n en trs/s

T en N.m

en Wb Remarque: On note aussi C

T dépend de I et de .

Si  est une constante, alors T ne dépendra que du courant I.

T = K.I

Remarque: T et  sont interdépendants par l’intermédiaire de I.

En effet, si I augmente, n diminue.

Couple résistant des génératrices:

Lorsqu’une génératrice débite, ses conducteurs sont traversés par un courant, donc soumis à une force électromagnétique.

Cette force crée un couple qui, s’il était seul, ferait tourner l’induit en sens inverse de celui qu’on lui impose.

Dans des conditions identiques, le couple résistant d’une génératrice aura le même moment que le couple d’un moteur, puisque les conducteurs seront traversés par le même courant et placés dans le même flux.

T_r = NI/2

C’est pour vaincre ce couple résistant que le moteur d’entraînement doit fournir de la puissance à la génératrice.

Coexistence des deux phénomènes:

Les deux phénomènes, induction électromagnétique (fem) et forces électromagnétiques, coexistent toujours quel que soit l’usage de la machine.

Égalité des puissances:

T = kI

EI = kI

Nécessité du rhéostat de démarrage:

Expression du courant dans l’induit:

Sachant que: U = E + RI

I = (U – E)/R = (U – Nn)/R

Si le flux  est constant, le courant I ne dépend que de la vitesse de rotation.

Démarrage:

Au moment du démarrage, la vitesse de rotation et la f.e.m sont nulles.

Par conséquent, le courant n’est limité que par la résistance de l’induit R:

I_d = U/R

Un induit qui ne tourne pas se comporte comme un résistor pur.

Exemple:

Sur la plaque signalétique d’un moteur à courant continu, on trouve:

n_N = 1500 trs/min

U_N = 120 V

I_N = 33 A

P_N = 3,3 kW

R = 0,3 .

Le calcul de I_d donne:

I_d = U/R = 120/0,3 = 400 A.

Cette intensité représente plus de 12 fois I_N.

C’est une valeur dangereuse pour l’induit.

Solution:

Il est évident qu’une limitation du courant de démarrage s’impose.

On insère un rhéostat R_h en série avec l’induit pour limiter le courant Id à la valeur :

I_d = U/(R + R_h)

Si on se limite, par exemple, à

I_d = 2I_N

Ce qui est tolérable, le rhéostat aura pour valeur:

R_h = U/2I_N – R

Remarque: Le rhéostat de démarrage comporte plusieurs plots, et R_h correspond à sa valeur maximale.

En charge:

Construction de la caractéristique n=f(I)

Sachant que :

E = nN = U – RI

et

n = (U – RI)/N

à vide, on a

et

Ce qui nous permet d’écrire:

Soit:

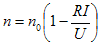
Pour un moteur à flux constant, la vitesse est une fonction linéaire décroissante du courant absorbé.

Caractéristiques électromécaniques de couple:

Couple électromagnétique : Il ne dépend que du courant absorbé et du flux:

T = NI/2

A excitation constante, donc à flux constant, on a:

T = KI

T=f(I) est une droite passant par l’origine:

C’est la caractéristique électromécanique de couple. Elle est tracée à U et i constantes.

Couple utile: la puissance mécanique utile, celle qui est disponible sur l’arbre du moteur, est égale à la puissance électrique utile diminuée des pertes collectives.

Le couple utile est donc légèrement inférieur au couple électromagnétique.

La diminution est pratiquement indépendante de I.

Le couple utile est donc représenté par une droite parallèle à celle du couple électromagnétique.

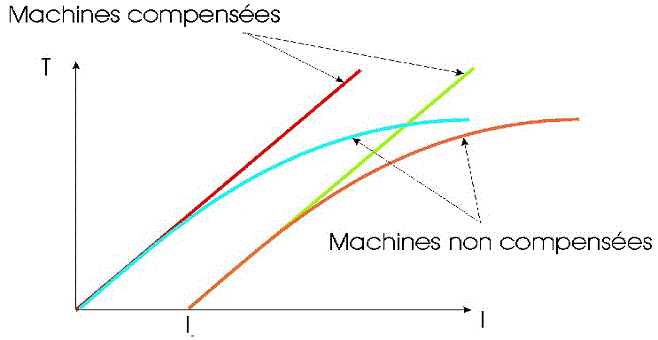
Caractéristique mécanique de couple électromagnétique: T(n), T()

T = k(U – Nn)/R

U et i : constants, donc  constant

T est une fonction linéaire décroissante de n ()

Caractéristique mécanique de couple électromagnétique: T(n), T()

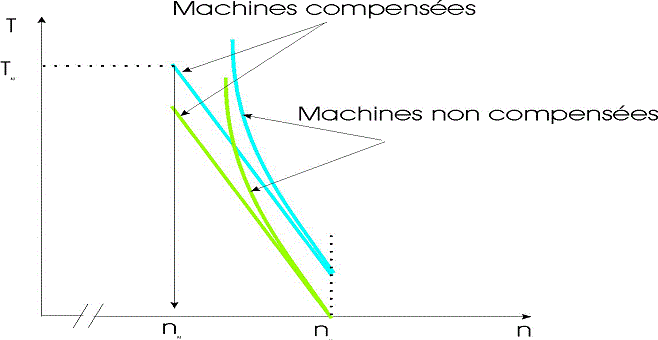
Caractéristique mécanique de couple électromagnétique: T(n), T()

La puissance électromagnétique est la puissance transformée, elle s’écrit:

P_em = T_em. = E_ch.I = U.I – R.I²

Si l’on tient compte de la réaction d’induit,

T_em = k(I,i).I

Caractéristique mécanique de couple électromagnétique: T(n), T()

Dans le fonctionnement à vide, les pertes constantes et le couple de pertes ont pour expression:

U.I₀ = p_m + p_f + R.I₀²

Or I₀ est très faible et RI₀² l’est aussi devant U.I₀

Caractéristique mécanique de couple électromagnétique: T(n), T()

Ce qui nous permet d’écrire:

U.I₀ # p_m + p_f = T_p.

P_m et p_f sont respectivement les pertes mécaniques et les pertes fer.

Caractéristique mécanique de couple électromagnétique: T(n), T()

A partir des expressions précédentes, on écrit:

T_u = T_em – T_p

Où T_u est le couple utile.

Bilan énergétique:

Puissance absorbée:

C’est la somme des puissances absorbées par le circuit induit et par le circuit inducteur.

Pour l’induit:

P = U.I

Pour l’inducteur:

p = u.i

Au total:

P_a = U.I + u.i

Pertes:

Ces pertes sont dues, à la fois, à l’effet magnétique à cause de la rotation du rotor dans le champ magnétique et au frottement et à la ventilation.

On les appelle pertes collectives et on les note p_c.

En plus de ces pertes s’ajoutent celles par effet Joule dans l’induit et dans l’inducteur:

p_jr = R.I²

p_e =u.i

Puissance mécanique utile:

C’est la puissance disponible sur l’arbre du moteur:

Putile = Pabsorbée – pertes

Pu = (U.I + u.i) – (R.I² + u.i + p_c)

Pu = U.I – R.I² – p_c

En tenant compte de la relation

E = U – R.I

P_u = (U – R.I).I – p_c = E.I – p_c

Le produit E.I est la puissance électrique utile.

P_u = P_eu – p_c

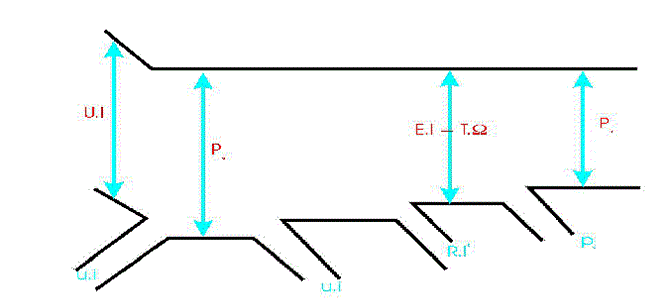
Rendement:

 = P_u/P_a =(Peu –pc)/(U.I + u.i)