Modélisation et rendement du moteur asynchrone triphasé

Le moteur asynchrone triphasé est constitué de deux parties principales:

• Une fixe appelée « STATOR »;

• Une mobile appelée « ROTOR.

Ces deux parties sont séparées par un espace appelé « entrefer »;

Le « STATOR » et le « ROTOR » sont des circuits composés d'enroulements formant des spires électromagnétiques, sièges d'un champ magnétique.

Le « STATOR » représente le circuit récepteur triphasé, il permet de créer un champ magnétique tournant dans l'enceinte de la machine;

Ce champ évolue à la fréquence de la source d'alimentation triphasée;

Le « ROTOR » est un circuit fermé sur lui-même, donc court-circuité, il se trouve immergé dans le champ magnétique tournant créé par le « STATOR »;

Il est, alors, le siège de courants induits de Foucault, tendant à s'opposer à la cause qui leur a donné naissance, soit une rotation;

Le « ROTOR » est entraîné, donc, en mouvement de rotation dans le sens de celui du champ tournant.

Le moteur est un convertisseur électromécanique permettant de convertir une énergie électrique en une énergie mécanique moyennant un champ magnétique;

On peut alors admettre que l'ensemble « STATOR - ROTOR » est équivalent à un TRANSFORMATEUR dont l'enroulement primaire est le « STATOR » et l'enroulement secondaire est le « ROTOR » .

Représentation du transformateur statique:

V₁: tension primaire

I₁: courant primaire

N₁: nombre de spires de l'enroulement primaire

V₂: tension secondaire

I₂: courant secondaire

N₂: nombre de spires de l'enroulement secondaire

est le flux magnétique commun au primaire et au secondaire

m est le rapport de transformation du transformateur, m=N₂/N₁

Le circuit électrique équivalent au transformateur est le suivant:

Ce schéma est une représentation du transformateur réel.

Il tient compte de:

• L'impédance de l'enroulement primaire (l₁, r₁);

• L'impédance magnétisante (L_F, R_F);

• L'impédance de l'enroulement secondaire (l₂, r₂).

Le rôle du transformateur statique est de modifier l'amplitude de la tension et celle de l'intensité du courant, sans pour autant, modifier la fréquence.

La transformation se fait avec conservation de la puissance, à des pertes fer et cuivre près.

Modélisation de la machine asynchrone :

Le moteur asynchrone est similaire, du point de vue constitution, au transformateur statique, à quelques différences près:

Les fréquences au primaire et au secondaire ne sont pas les mêmes :

• Le moteur fournit aussi de la puissance mécanique;

• Le rapport de transformation est variable;

Compte tenu de ces considérations, le schéma équivalent du moteur peut être fait dans les deux cas: à l'arrêt et en rotation.

De même, à l'arrêt, il peut être à rotor ouvert ou en court-circuit (bloqué);

Et en rotation, il peut être à vide ou en charge.

Remarque:

Seul l'enroulement du rotor du moteur à bagues (rotor bobiné) peut être ouvert;

Le rotor du moteur à cage n'est pas accessible, mais son étude reste faisable.

Le schéma équivalent est, comme dans le cas du transformateur triphasé, pris sur une seule phase.

Moteur à l'arrêt, rotor ouvert, g=1

Moteur à l'arrêt, rotor ouvert, g=1

Équations mises en jeu:

Tension au primaire ( convention récepteur):

Tension au secondaire ( convention générateur):

Rapport de transformation :

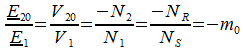
Moteur à l'arrêt, en court-circuit, rotor bloqué, g=1

Si on alimente le stator, circuit primaire, sous sa tension nominale, les courants primaire et secondaire seront tellement élevés que les enroulements seront rompus et enduit fondu.

Il faut absolument travailler sous tension réduite, le courant secondaire ne doit pas dépasser le courant nominal;

I_2CC = I_2N

Équations mises en jeu:

soit:

et

De même, on a, pour une phase:

R_S est ramenée au secondaire (x m₀²).

Moteur à rotor bobiné en rotation, g≠1

Le rapport de transformation devient:

et par conséquent:

de même, la pulsation (fréquence) devient:

et

Le schéma équivalent du moteur devient:

Équations mises en jeu:

Équation qu'on peut écrire aussi:

Comparée à celle obtenue à l'arrêt du rotor, g=1, on peut dire qu'un rotor fictif présentant une résistance R/g tourne à la même vitesse que le champ tournant, (la fréquence des courants rotoriques est égale à celle des courants statoriques).

Schéma équivalent ramené au primaire:

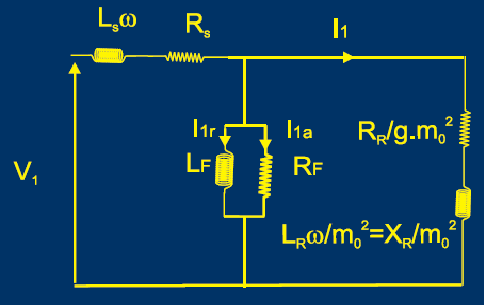
Ramener une impédance du secondaire au primaire revient à la diviser par le carré du rapport de transformation et inversement.

Puissance transmise au rotor:

On a, pour une phase:

P_e: puissance transmise au rotor ou puissance électromagnétique;

I₁ : courant primaire;

I₂ : courant secondaire;

P_e = (R_R/g.m²₀).I₁² = (R_R/g).I₂²

Pertes par effet Joule au rotor:

Soit:

Puissance mécanique:

C'est la différence:

La résistance ramenée au primaire correspond aux pertes Joule au rotor;

La résistance correspond à la puissance mécanique du moteur.

Très important!!!

Les puissances sont exprimées pour une seule phase, pour évaluer les puissances du moteur, il faut multiplier par 3.

Rendement du moteur asynchrone

Le bilan des puissances pour un moteur asynchrone peut être illustré de la façon suivante:

Le rotor reçoit la puissance .

Avec

Ce qui donne:

De même:

Soit:

N.B: Bien faire la différence entre une phase et le moteur entier.

Bilan des pertes:

Les puissances perdues dans un moteur en fonctionnement sont de type:

• Électrique: résistances des enroulements ;

  • Effet Joule au stator;

  • Effet Joule au rotor;

• Magnétique: existence de champ variable

  • Pertes dans le fer au stator;

  • Pertes dans le fer au rotor, très souvent négligés;

• Mécanique: rotation du rotor

  • Par frottement, ventilation.

Les pertes par effet Joule, peuvent être déterminées lors d'un essai en charge, ou en court-circuit:

Les pertes dans le fer peuvent être déterminées à partir d'un essai à vide;

Les pertes mécaniques peuvent être déterminées à partir d'un essai à vide;

Sachant que:

Pour connaître P_f et P_m, il faut faire une séparation des pertes.

En effet, on sait que:

• P_m est constante, elle ne dépend que de la structure de la machine;

• P_f est fonction linéaire du carré de la tension;

Par conséquent, quelque soit la valeur de la tension d'alimentation, P_m reste inchangée et P_f croit linéairement en fonction de U².

La courbe peut se présenter de la façon suivante:

• A est le point de décrochage du moteur;

• On prolonge jusqu'à l'intersection avec l'axe des puissances, c'est la puissance mécanique P_m;

• Au point de fonctionnement donné, on soustrait P_m de P₁₀ pour avoir P_f.

Dans le cas d'un moteur asynchrone à rotor bobiné, la puissance à vide à rotor ouvert représente la puissance perdue dans le fer: P₁₀ = P_f

Une autre évaluation de P_m et P_f, c'est de considérer que :

P_m = P_f = 1/2.P₁₀

C'est une estimation à prendre avec beaucoup de prudence.

Pertes totales:

Puissance absorbée:

Rendement:

Étude du couple électromagnétique

Il a été établi que:

De même:

Soit:

Qu'on peut écrire aussi:

Si l'on pose:

Le couple devient:

La courbe de variation de cette équation est donnée pour g compris entre 0 et 1.

Cette courbe passe par un maximum de glissement qui vaut:

Sa valeur est:

On peut utiliser la vitesse de rotation W au lieu du glissement g.

Dans ce cas:

• si g=0,  ;

• si g=1,  ;

La courbe est alors inversée.

Le couple de démarrage est obtenu à g=1 ().

Variation du courant rotorique en fonction de g

A partir de la relation ci-dessous, déjà établie:

Ce qui donne, en module:

Qu'on peut écrire aussi:

Quelques procédés de démarrage des moteurs asynchrones

Le courant de démarrage est obtenu pour g=1 ().

Ce courant peut atteindre des valeurs trop élevées, c'est la raison pour laquelle, un démarrage progressif est conseillé, voire imposé.

Cas du moteur à cage:

• Direct;

• Par élimination de résistances statoriques;

• Auto-transformateur;

• Étoile-triangle;

Exemple de démarrage étoile-triangle

Étoile :

• Tension :

• Courant :

Triangle :

• Tension :

• Courant :

D'où,

et

Le couple étant proportionnel au carré du courant, donc:

Cas du moteur à rotor bobiné:

• Démarrage par élimination de résistances rotoriques (le plus utilisé et le plus économique);

• Cascade hyposynchrone;

• Démarrage par élimination de résistances rotoriques;

La valeur de la résistance au niveau du rotor est augmentée, le courant, lui, devient réduit, le couple aussi.

En éliminant progressivement les résistances en série, une à une, le courant augmente, le couple, quant à lui, varie peu.

Lors du démarrage, les résistances consomment une puissance importante par effet Joule, le rendement du moteur au démarrage est mauvais.

Démarrage par élimination de résistances rotoriques;

L'ajout de résistances au niveau du rotor provoque la diminution du courant dans le rotor, mais une augmentation du couple.