Moteur à excitation série

Constat préliminaire

Le moteur à excitation série a la particularité d’avoir un inducteur qui est traversé par le même courant que l’induit, donc beaucoup plus important que celui des machines à excitation indépendantes (shunt).

L’inducteur possède donc une résistance plus faible que celle des autres types de machines.

En raison du courant d’excitation élevé et pour avoir un flux du même ordre que celui dans les autres types de machines, le nombre de spires doit être diminué et la section doit être augmentée.

D’où une résistance plus faible.

Équations du moteur

Machine en charge:

U = E + (R + r).I

avec

E =k(I)N : la f.e.m en charge et  le flux magnétique sous un pôle.

U = kN + (R + r).I

Donc:

N = (U - (R + r).I)/k

A vide: I # 0,

donc (I)=0 et N tend vers l’infini.

Un moteur à excitation série ne doit jamais fonctionner à vide sous tension nominale.

Caractéristique de la vitesse

Sachant que:

U = E + (R + r).I = k(I)N + R_t.I

E représente la f.e.m en charge.

R_t est la résistance équivalente de l’induit en série avec l’inducteur.

D’après la loi d’Ohm, et compte tenu de la relation:

E_ch = kN(I), on a:

Quand I tend vers 0, N=/I.

Le moteur s’emballe.

Quand  est constant, forte saturation, N=(U – R_t.I).

La caractéristique est linéaire, mais cela n’est observable qu’au dessus du courant nominal.

Caractéristique de couple T(I)

P_em = T_em. = E.I

De même:

E = kI

et

T_em = k(I).I

Caractéristique mécanique T(n)

A partir des deux caractéristiques précédentes on déduit celle de T(n).

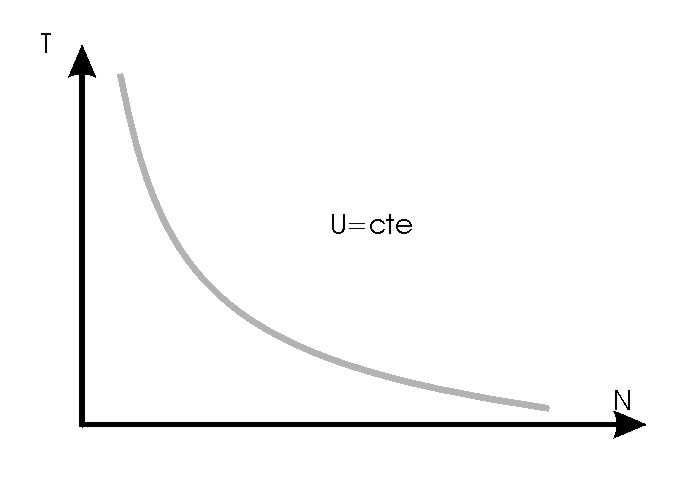
Réglage de la vitesse de rotation

Pour réduire le flux magnétique par pôle, et augmenter la vitesse dans des proportions raisonnables, on place un rhéostat en parallèle avec l’inducteur.

On a:

où s < 1

A partir de ce paramètre, on déduit les différentes caractéristiques.

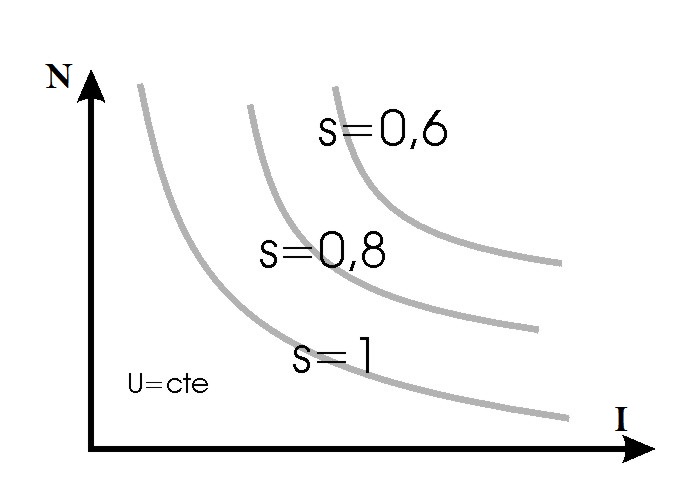
Bilan énergétique et rendement

Puissance absorbée:

Pa = U.I = (E + R_t.I).I

Pertes par effet joule: R_t.I²

Pertes collectives: p_c

Puissance électrique utile: P_eu = E.I

Puissance utile: Pu=U.I – R_t.I² - p_c = E.I – p_c

Rendement

 = P_u/P_a=(E.I – p_c)/U.I