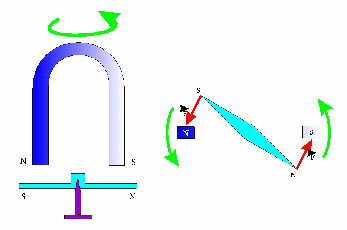
Champ magnétique tournant
Étude expérimentale des champs tournants
Champ tournant produit par un aimant permanent:
Action sur une aiguille aimantée:

L’aiguille tourne à la même fréquence de rotation que l’aimant.
On dit qu’elle tourne au synchronisme.
Il y a attraction mutuelle des pôles de noms contraires: développement d’un couple moteur.
Action sur un disque non magnétique:
L’aiguille est remplacée par un disque non magnétique (en cuivre ou en aluminium).

La rotation de l’aimant produit celle du disque.
Mais le disque tourne plus lentement que l’aimant.
Le disque n’est pas synchrone, il est dit asynchrone.
Comment un disque non aimanté est-il entraîné par l’aimant?
Le déplacement de l’aimant induit des courants de Foucault, qui doivent s’opposer à la cause qui leur a donné naissance: loi de Lenz.
Cette cause est le déplacement relatif de l’aimant par rapport au disque.
Ces courants induits ne peuvent empêcher la rotation réelle de l’aimant. Ils entraînent le disque dans un mouvement permettant de diminuer le déplacement relatif du champ, soit une rotation.
Un couple moteur est donc créé entre les pôles de l’aimant et les pôles développés par les courants induits.
Y a-t-il synchronisme?
Si oui, il y aurait immobilité du disque par rapport à l’aimant,
donc pas de déplacement relatif
alors pas de courants induits
pas de déplacement du disque
il y a déplacement relatif
il y a création de courants de Foucault
etc,
Le disque tourne nécessairement à une fréquence de rotation inférieure à celle du champ magnétique.
Généralisation
Un champ tournant peut être créé par :
un aimant permanent;
un enroulement alimenté en courant continu;
un enroulement alimenté en courant alternatif;
Champ tournant produit par enroulement alimenté par un courant sinusoïdal monophasé:
Action sur une aiguille aimantée:
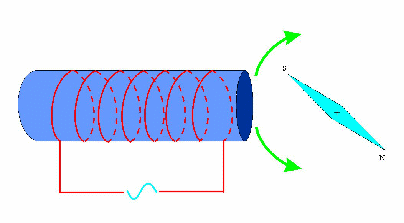
La rotation de l’aiguille deviendra possible, si l’on donne un coup pour la lancer dans un sens.
Elle va continuer à tourner à la même fréquence que celle du générateur sinusoïdal.
Superposition de deux champs égaux:
Suivant la direction de l’axe de la bobine, la valeur du champ b est:
![]()
On peut envisager deux vecteurs champ magnétique de valeur maximale Bmax /2 qui évoluent à la pulsation w, mais en sens opposés.
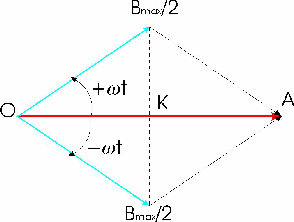
Dans ce cas, on a:
![]()
C’est le théorème de Leblanc .
Action sur un disque métallique:
Le disque reste immobile, sauf si on le lance en rotation, il continuera à tourner lentement.
Amélioration du système:

Assurer la symétrie du champ magnétique et celle des actions mécaniques sur l’aiguille ou le disque.
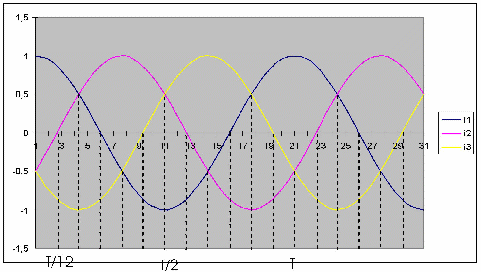
Champ tournant produit en triphasé

Les trois bobines sont identiques et disposées à 120° l’une de l’autre.
Elles sont traversées par des courants triphasés.
Une aiguille aimantée placée au centre du système se met à tourner spontanément et atteint la fréquence des tensions: n=f
Un disque métallique tourne aussi de lui-même, mais à vitesse réduite.
La permutation de deux fils d’alimentation inverse le sens de rotation.
Conclusion
En monophasé, il faut lancer la partie tournante;
En triphasé, la rotation se fait spontanément dans un sens déterminé;
Le couple développé permet la rotation synchrone de l’aiguille aimantée et asynchrone du disque.
Étude champ tournant produit par des courants triphasés:
Système étudié:
Partie tournante: rotor bipolaire et possédant des enroulements alimentés en courant continu;
partie fixe: stator ferromagnétique siège d’un champ tournant (donc feuilleté) et possédant trois enroulements disposés de 120° l’un de l’autre alimentés en triphasé;

|
|
0 |
T/12 |
2T/12 |
3T/12 |
4T/12 |
5T/12 |
6T/12 |
7T/12 |
8T/12 |
9T/12 |
10/12 |
11T/12 |
T |
|
b1 |
Bm |
0,866Bm |
Bm/2 |
0 |
-0,5Bm |
|
|
|
|
|
|
|
|
|
b2 |
-Bm/2 |
0 |
Bm/2 |
0,866Bm |
Bm |
|
|
|
|
|
|
|
|
|
b3 |
-Bm/2 |
-0,866Bm |
-Bm |
-0,866Bm |
-0,866Bm |
|
|
|
|
|
|
|
|
|
A t=0 |
A t=T/12 |
A t=2T/12 |
A t=3T/12 |
|
|
|
|
|
|
|
Expression du champ tournant:
Champ produit par un enroulement unique:
Avec un courant continu:
L’entrefer a une largeur constante, le champ y est radial.
La valeur du champ dépend de la position angulaire d’un point donné.
La répartition est donc sinusoïdale.
![]()
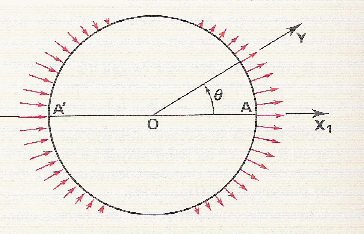
Avec un courant sinusoïdal:
Le champ dépend, à la fois de la position angulaire du point et du temps.
Champ créé par l’enroulement:
![]()
![]()
Valeur du champ à une position angulaire donnée:
![]()
Soit,
![]()
|
Aspect du champ à un instant donné: (t=0) |
Aspect du champ dans le temps : C’est une onde stationnaire |
|
|
|
Décomposition mathématique du champ:
![]()
Donc:
![]()
Théorème de Leblanc.
Champ produit par un système triphasé
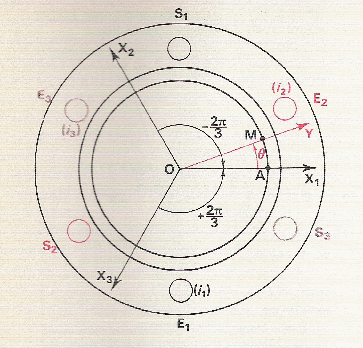
![]()
![]()
![]()
![]()
![]()
![]()
b = b1 + b2 + b3
![]()
C’est une onde progressive d’amplitude 3Bmax/2.
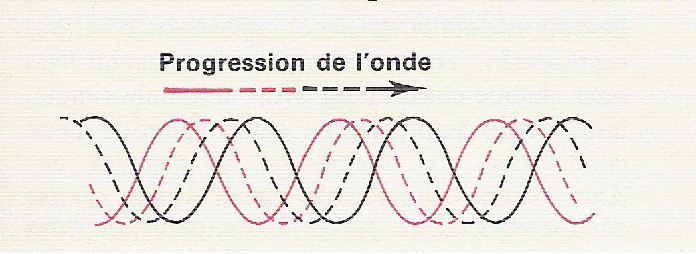
Le
champ glisse dans l’entrefer à la vitesse angulaire
![]()
La fréquence de rotation d’un rotor à 2p pôles est:
n=f/p